Trochiscanthe nodiflore n°532 (2016-32)

Suggestion de lecture :

LES ÉPEIRES

GÉOMÉTRIE DE LA TOILE

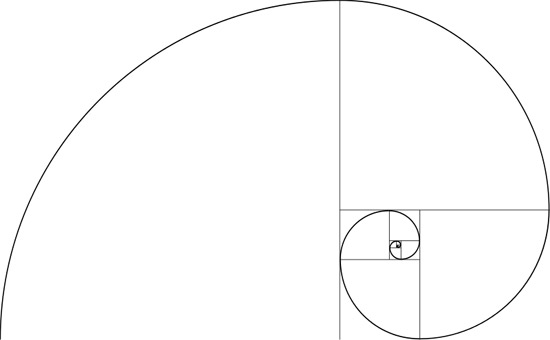
Me voici aux prises avec un chapitre à la fois d'un haut intérêt et d'une rédaction difficultueuse : non que le sujet soit obscur, mais il suppose, chez le lecteur, une certaine dose de géométrie, forte nourriture trop négligée. Je ne m'adresse pas à des géomètres, en général peu soucieux des choses de l'instinct ; je ne m'adresse pas non plus à des entomologistes collectionneurs, eux-mêmes indifférents aux théorèmes mathématiques ; j'écris pour toute intelligence capable de prendre goût aux leçons de l'insecte.

Comment faire ? Supprimer ce chapitre, ce serait négliger le trait le plus remarquable de l'industrie arachnéenne ; le traiter comme il le mérite avec l'appareil de formules savantes, ce serait entreprise déplacée en ces modestes pages. Prenons un moyen terme ; ni vérités abstruses, ni complète ignorance.

Portons notre attention sur les réseaux des Épeires, de préférence sur ceux de l'Épeire soyeuse et de l'Épeire fasciée, si fréquents en automne dans ma région et si remarquables d'ampleur. Nous reconnaîtrons d'abord que les rayons sont équidistants ; ils forment de l'un à l'autre des angles sensiblement égaux, et cela malgré leur multiplicité, qui dépasse la quarantaine dans l'ouvrage de l'Épeire soyeuse. Nous avons vu par quelle étrange méthode l'Aranéide parvient à ses fins : diviser l'aire où doit s'ourdir le filet en un nombre considérable de secteurs d'égale ouverture, nombre à peu près constant pour chaque espèce. Une manoeuvre sans ordre, régie, dirait-on, par un fougueux caprice, a pour résultat une belle rosace digne de notre compas.

Nous reconnaîtrons aussi que, dans chaque secteur, les divers échelons, éléments des tours de spire, sont parallèles entre eux et deviennent, petit à petit, plus rapprochés les uns des autres à mesure qu'ils sont situés plus avant vers le centre. Avec les deux rayons qui les limitent, ils forment d'un côté un angle obtus et de l'autre un angle aigu, angles qui se maintiennent constants dans le même secteur, à cause du parallélisme.

Il y a plus : d'un secteur à l'autre, ces mêmes angles, l'obtus comme l'aigu, ne changent pas de valeur, autant que peuvent en juger les scrupules du regard seul. En son ensemble, l'édifice funiculaire est dont une série de traverses qui coupent obliquement les divers rayons sous des angles de valeur invariable.

A ce caractère se reconnaît la spirale logarithmique. Les géomètres appellent de ce nom la courbe qui coupe obliquement, sous des angles de valeur constante, toutes les droites ou rayons vecteurs s'irradiant d'un centre appelé pôle. Le tracé des Épeires est donc une ligne polygonale inscrite dans une spirale logarithmique. Il se confondrait avec cette spirale si le nombre des rayons était illimité, ce qui rendrait les éléments rectilignes infiniment courts et changerait la ligne polygonale en une ligne courbe.

Désireux de faire entrevoir pourquoi cette spirale a tant exercé les méditations de la science, bornons-nous maintenant à quelques énoncés dont le lecteur trouvera la démonstration dans les traités de géométrie supérieure.

La spirale logarithmique décrit un nombre sans fin de circuits autour de son pôle, dont elle se rapproche toujours sans pouvoir y parvenir. Ce point central, à chaque tour plus voisin, est indéfiniment inaccessible. Il va de soi que cette propriété n'est pas du domaine de nos sens. Même aidée des meilleurs instruments de précision, la vue ne pourrait suivre ses interminables circuits, et renoncerait bientôt à poursuivre la division de l'invisible. C'est un enroulement auquel l'esprit ne conçoit pas de bornes. Seule, la raison cultivée, plus perspicace que notre rétine, voit en pleine clarté ce qui défie la perception du regard.

L'Épeire se conforme de son mieux à cette loi de l'enroulement illimité. Les tours de spire se serrent d'avantage l'un de l'autre en se rapprochant du pôle. A une certaine distance, brusquement ils s'arrêtent ; mais alors fait suite au fil la spirale auxiliaire, non détruite dans la région centrale, et l'on voit, non sans quelque surprise, celle-ci continuer d'avancer vers le pôle en tours de plus en plus serrés, à peine discernables. Ce n'est pas, bien entendu, la rigueur mathématique, mais une approximation très nette de cette rigueur. L'Épeire cerne son pôle de plus en plus près, autant que le lui permet son outillage, défaillant comme le nôtre. On la dirait versée à fond dans les lois de la spirale.

Continuons d'énoncer sans explications quelques-unes des propriétés de la curieuse courbe. Imaginons un fil flexible enroulé sur la spirale logarithmique. Si nous le déroulons en le tenant toujours tendu, son extrémité libre décrira une spirale en tout pareille à la première. La courbe aura seulement changé de place.

Jacques Bernouilli, à qui la géométrie doit ce magnifique théorème, fit graver sur sa tombe, comme un de ses beaux titres de gloire, la spirale génératrice et sa pareille engendrée par le déroulement du fil. Une inscription disait : Eadem mutata resurgo, je ressuscite identique à moi-même. Difficilement la géométrie trouverait mieux que cette superbe envolée vers le grand problème de l'au-delà.

On connaît une autre épitaphe géométrique non moins célèbre. Cicéron, étant questeur en Sicile, cherchait, parmi les ronces et les folles herbes qui font sur nous l'oubli, la tombe d'Archimède, et la reconnut, au milieu des ruines, à la figure géométrique gravée sur la pierre : le cylindre circonscrit à la sphère. Le premier, en effet, Archimède connut le rapport approximatif de la circonférence au diamètre ; il en déduisit le périmètre et la surface du cercle, ainsi que la surface et le volume de la sphère. Il démontra que cette dernière a pour surface et pour volume les deux tiers de la surface et du volume du cylindre circonscrit. Dédaigneux d'inscription pompeuse, le savant Syracusain se glorifia de son théorème pour toute épitaphe. La figure géométrique disait le nom du personnage aussi clairement que l'auraient fait des caractères alphabétiques.

Pour en finir, encore une propriété de la spirale logarithmique. Faisons rouler la courbe sur une droite indéfinie. Son pôle se déplacera en se maintenant toujours sur une même ligne droite. L'enroulement sans fin conduit au trajet rectiligne ; le perpétuellement varié engendre l'uniforme.

Or, cette spirale logarithmique, si curieuse de propriétés, est-elle une simple conception des géomètres, combinant à leur gré le nombre et l'étendue pour imaginer un abîme ténébreux où s'exercent après leurs méthodes de sondage ? Est-ce une pure rêverie dans la nuit du difficile, une énigme abstraite jetée en pâture à notre entendement ?

Non, c'est une réalité au service de la vie, un tracé dont l'architecture animale fréquemment fait usage. Le Mollusque, en particulier, n'enroule jamais la rampe à vis de la coquille sans consulter la savante courbe. Les premiers-nés de la série l'ont connue et pratiquée, aussi parfaite aux premiers âges du monde qu'elle peut l'être aujourd'hui.

Etudions, à ce sujet, les Ammonites, vénérables reliques de ce qui fut autrefois la plus haute expression des vivants, lorsque s'ébauchait la terre ferme avec les boues océaniques exondées. Taillé et poli dans le sens de sa longueur, le fossile nous montre une superbe spirale logarithmique, norme générale de l'habitation qui fut un palais de nacre, à chambres multiples traversées d'un siphon.

Aujourd'hui, le dernier représentant des Céphalopodes à coquille cloisonnée, le Nautile des mers de l'Inde, reste fidèle à l'antique devis ; il n'a pas trouvé mieux que ses lointains prédécesseurs. Il a changé le siphon de place, l'a mis au centre au lieu de le laisser sur le dos, mais il enroule toujours logarithmiquement sa spire comme le pratiquaient les Ammonites aux premiers âges du monde.

Et n'allons pas croire que ces princes des Mollusques aient le monopole de la savante courbe. Dans les eaux tranquilles de nos fossés herbeux, les coquillages aplatis, les humbles Planorbes, parfois guère plus grands qu'une lentille, rivalisent de haute géométrie avec l'Ammonite et le Nautile. Tel d'entre eux, le Planorbis vortex, par exemple, est une merveille d'enroulement logarithmique.

Dans les coquillages de forme allongée, la structure devient complexe, tout en étant soumise aux mêmes lois fondamentales. J'ai sous les yeux quelques espèces du genre Terebra, venues de la Nouvelle-Calédonie. Ce sont des cônes très effilés, d'une longueur atteignant presque l'empan. La surface en est lisse, toute nue, sans aucun des ornements habituels, plis, nodosités, cordons de perles. L'édifice spiral est superbe, uniquement paré de sa simplicité. J'y compte une vingtaine de tours qui, par degrés, s'amoindrissent et se perdent dans les délicatesses de la pointe. Un fin sillon les délimite.

Je trace au crayon une génératrice quelconque de ce cône, et, m'en rapportant au seul témoignage de ma vue, quelque peu exercée aux mensurations géométriques, je trouve que le sillon spiral coupe cette génératrice sous un angle de valeur constante.

La conséquence de ce résultat est facile à déduire. Par projection sur un plan perpendiculaire à l'axe de la coquille, les génératrices du cône deviendraient des rayons, et le sillon qui monte en tournant de la base au sommet se convertirait en une courbe plane qui, rencontrant les rayons sous un angle invariable, ne serait autre qu'une spirale logarithmique. Inversement, on peut considérer le sillon de la coquille comme la projection de cette spirale sur une surface conique.

Il y a mieux. Concevons un plan perpendiculaire à l'axe de la coquille et passant par le sommet. Imaginons en outre un fil enroulé sur le sillon spiral. Déroulons-le en le tenant tendu. Son extrémité ne sortira pas du plan et y décrira une spirale logarithmique. C'est, à un degré plus grand de complication, une variante de l'eadem mutata resurgo de Bernouilli : la courbe à logarithmes conique se change en courbe à logarithmes plane.

Semblable géométrie se retrouve dans les autres coquilles en cône allongé, les Turritelles, les Fuseaux, les Cérithes, ainsi que sur les coquilles en cône surbaissé, les Troques, les Turbo. Ne font pas exception les globuleuses, les enroulées en volute. Toutes, jusqu'au trivial Escargot, sont construites dans l'ordre logarithmique. La spirale célèbre parmi les géomètres est le plan général suivi par le Mollusque enroulant son étui de pierre.

D'où provient telle science chez ces glaireux ? — On nous dit : le Mollusque dérive du Ver. Or, un jour, émoustillé par le soleil, le Ver s'émancipa, brandit sa queue, la tire-bouchonna d'allégresse. Du coup était trouvé le plan de la future coquille spiralée.

Voilà ce qui s'enseigne très sérieusement aujourd'hui, comme le dernier mot du progrès scientifique. Reste à savoir jusqu'à quel point l'explication est acceptable. Pour sa part, l'Araignée n'en veut absolument pas. Non parente du Ver, dépourvue d'appendice apte à se tire-bouchonner, elle connaît cependant la spire à logarithmes. De la célèbre courbe, elle n'obtient qu'une sorte de charpente ; mais, tout élémentaire qu'elle est, cette charpente affirme clairement l'édifice idéal. L'Épeire travaille d'après les mêmes principes que le Mollusque à coquille convolutée.

Ce dernier, pour construire sa spire, a des années entières, et il met dans l'enroulement une perfection exquise. L'Épeire pour tendre son réseau, n'a qu'une séance d'une heure au plus ; aussi la rapidité de l'exécution lui impose-t-elle ouvrage plus simple. Elle abrège, en se bornant au croquis de la courbe que l'autre décrit en pleine perfection.

L'Épeire est donc versée dans les secrets géométriques de l'Ammonite et du Pompile ; elle pratique, en la simplifiant, la ligne à logarithmes chère à l'Escargot. Quel est son guide ? Nul moyen d'invoquer ici un tortillement quelconque, comme on le fait au sujet du Ver, ambitieux de devenir Mollusque. Il faut nécessairement que la bête ait en elle-même le tracé virtuel de sa spirale. Jamais le hasard, si fécond que nous le supposions en surprises, n'a pu lui enseigner la haute géométrie où notre intelligence, sans forte culture préalable, ne tarde pas à s'égarer.

Convient-il de reconnaître dans l'art de l'Épeire un simple effet de l'organisation ? On songe volontiers aux pattes qui, douées d'une extension très variable, feraient office de compas. Plus ou moins fléchies, plus ou moins étalées, elles détermineraient machinalement l'angle sous lequel la spire doit couper le rayon : elles conserveraient le parallélisme des traverses dans chaque secteur.

Quelques objections se présentent, affirmant que l'outil n'est pas ici l'unique régulateur de l'ouvrage. Si la longueur des pattes déterminait l'arrangement du fil, on devrait trouver les tours de spire d'autant plus écartés l'un de l'autre que la filandière est plus longuement outillée. C'est ce que nous montrent, en effet, l'Épeire fasciée et l'Épeire soyeuse. La première, à pattes plus longues, écarte davantage ses traverses que ne le fait la seconde, à pattes plus courtes.

Mais ne comptons pas trop sur cette règle, nous disent les autres. L'Épeire angulaire, l'Épeire pâle et l'Épeire diadème, toutes les trois relativement courtaudes, rivalisent avec la svelte Épeire fasciée dans l'espacement de leurs gluaux. Les deux dernières les disposent même à des distances plus grandes.

Sous un autre rapport, on reconnaît que l'organisation n'impose pas immuable ouvrage. Avant d'entreprendre la spirale à gluaux, les Épeires en filent une première, simple auxiliaire destinée à fournir des points d'appui. Celle-ci, formée d'un fil ordinaire, non gluant, part du centre et aboutit à la circonférence par des tours d'ampleur rapidement croissante. C'est une construction provisoire dont il ne persiste que la partie centrale lorsque l'Araignée a posé ses gluaux. La seconde spirale, partie essentielle du piège, progresse, au contraire, en tours serrés, de la circonférence vers le centre, et se compose uniquement de traverses visqueuses.

Voilà donc, coup sur coup, par un brusque changement dans la mécanique, deux volutes d'ordre tout différent sous le rapport de la direction, du nombre de tours et de l'angle d'intersection. L'une et l'autre sont des spirales logarithmiques. Je ne vois aucun mécanisme des pattes, longues ou courtes, qui puisse rendre compte de ce changement.

Serait-ce alors, de la part de l'Épeire, combinaison préméditée ? Y aurait-il calcul, mensuration d'angles, vérification du parallélisme faite par le regard ou autrement ? J'incline à croire qu'il n'y a rien du tout, du moins rien d'autre qu'une propension innée, dont l'animal n'a pas à régler les effets, pas plus que la fleur ne règle l'agencement de ses verticilles. L'Épeire fait de la haute géométrie sans le savoir, sans y prendre garde. Cela marche tout seul, le branle étant donné par un instinct imposé dès l'origine.

Le caillou lancé par la main revient à terre en décrivant certaine courbe ; la feuille morte détachée et entraînée par un souffle d'air fait son trajet au sol suivant pareille courbe. Ni d'un côté ni de l'autre aucune intervention du mobile pour régler la chute ; néanmoins la descente s'accomplit suivant une trajectoire savante, la parabole, dont la section d'un cône par un plan a fourni le prototype aux méditations des géomètres. Une figure, d'abord simple aperçu spéculatif, devient réalité par la chute d'un caillou hors de la verticale.

Les mêmes méditations reprennent la parabole, la supposent roulant sur une droite indéfinie, et se demandent quel trajet suit alors le foyer de cette courbe. La réponse vient : le foyer de la parabole décrit une chaînette, ligne très simple de forme, mais dont le symbole algébrique doit recourir toutefois à une sorte de nombre cabalistique, brouillé avec toute numération et que l'unité se refuse à traduire, si loin qu'on la subdivise. On l'appelle le nombre e. Sa valeur est la série suivante, prolongée sans fin :

e = 1 + 1/1 + 1/1.2 + 1/1.2.3 + 1/1.2.3.4 + 1/1.2.3.4.5 + etc.

Si le lecteur avait la patience d'effectuer le calcul des quelques premiers termes de cette série, qui n'a pas de limites, puisque la série des nombres naturels n'en a pas elle-même, il trouverait :

e = 2,7182818...

Avec ce nombre étrange, sommes-nous cantonnés cette fois dans le strict domaine de l'imagination ? Pas du tout : la chaînette apparaît dans le réel toutes les fois que la pesanteur et la flexibilité agissent de concert. On appelle de ce nom la courbe suivant laquelle s'infléchit une chaîne suspendue en deux de ses points non situés sur la même verticale. C'est la forme d'un cordon souple que l'on abandonne à lui-même en tenant les deux bouts ; c'est la ligne qui régit la configuration d'une voile gonflée par le vent ; c'est la courbure de la sacoche à lait de la bique revenant de remplir sa traînante mamelle. Et tout cela fait appel au nombre e.

Que de science abstruse pour un bout de ficelle ! N'en soyons pas surpris. Un grain de plomb qui oscille à l'extrémité d'un fil, une goutte de rosée qui ruisselle le long d'une paille, une flaque d'eau qui se ride aux caresses de l'air, un rien, en somme, exige un échafaudage de Titans lorsqu'il faut y plonger le regard du calcul. Il nous faut la massue d'Hercule pour dompter un moucheron.

Certes, nos méthodes d'investigation mathématique sont ingénieuses ; on ne saurait trop admirer les puissantes cervelles qui les ont inventées ; mais combien lentes et pénibles en face des moindres réalités ! Ne nous sera-t-il jamais donné de scruter le vrai de façon plus simple ? L'intelligence pourra-t-elle un jour se passer du lourd arsenal des formules ? Pourquoi pas ?

Voici que l'abracadabrant nombre e reparaît, inscrit sur un fil d'Araignée. Considérons, par une matinée brumeuse, le réseau qui vient d'être construit pendant la nuit. A cause de leur hygrométrie, les gluaux se sont chargés de gouttelettes et, fléchissant sous le poids, sont devenus autant de chaînettes, autant de chapelets de gemmes limpides, gracieux chapelets rangés en ordre exquis et retombant en courbes d'escarpolette. Si le soleil perce le brouillard, l'ensemble s'illumine de feux diaprés et devient splendide girandole. Le nombre e est dans toute sa gloire.

La géométrie, c'est-à-dire l'harmonie dans l'étendue, préside à tout. Elle est dans l'arrangement des écailles d'un cône de pin comme dans l'arrangement des gluaux d'une Épeire, elle est dans la rampe d'un Escargot, dans le chapelet d'un fil d'Araignée, comme dans l'orbite d'une planète ; elle est partout, aussi savante dans le monde des atomes que dans le monde des immensités.

Et cette géométrie universelle nous parle d'un Universel Géomètre, dont le divin compas a tout mesuré. Comme explication de la logarithmique de l'Ammonite et de l'Épeire, j'aime mieux cela que le Ver se tortillant le bout de la queue. Ce n'est peut-être pas bien conforme aux enseignements d'aujourd'hui, mais c'est d'une plus haute envolée."

Jean-Henri FAVRE - Souvenirs entomologiques